optimization - How to show that the method of steepest descent does not converge in a finite number of steps? - Mathematics Stack Exchange
Por um escritor misterioso
Descrição
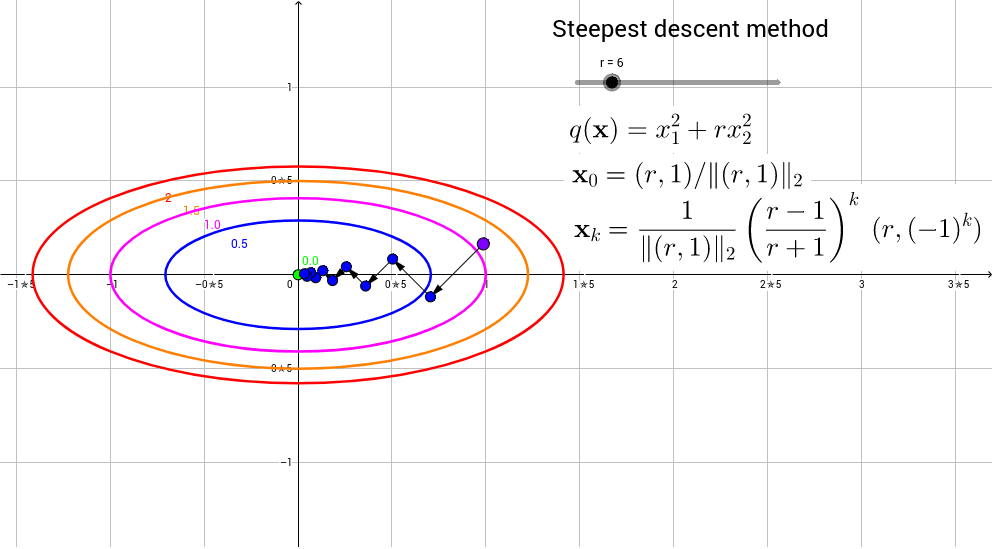
I have a function,
$$f(\mathbf{x})=x_1^2+4x_2^2-4x_1-8x_2,$$
which can also be expressed as
$$f(\mathbf{x})=(x_1-2)^2+4(x_2-1)^2-8.$$
I've deduced the minimizer $\mathbf{x^*}$ as $(2,1)$ with $f^*
Electronics, Free Full-Text
Bayesian optimization with adaptive surrogate models for automated experimental design
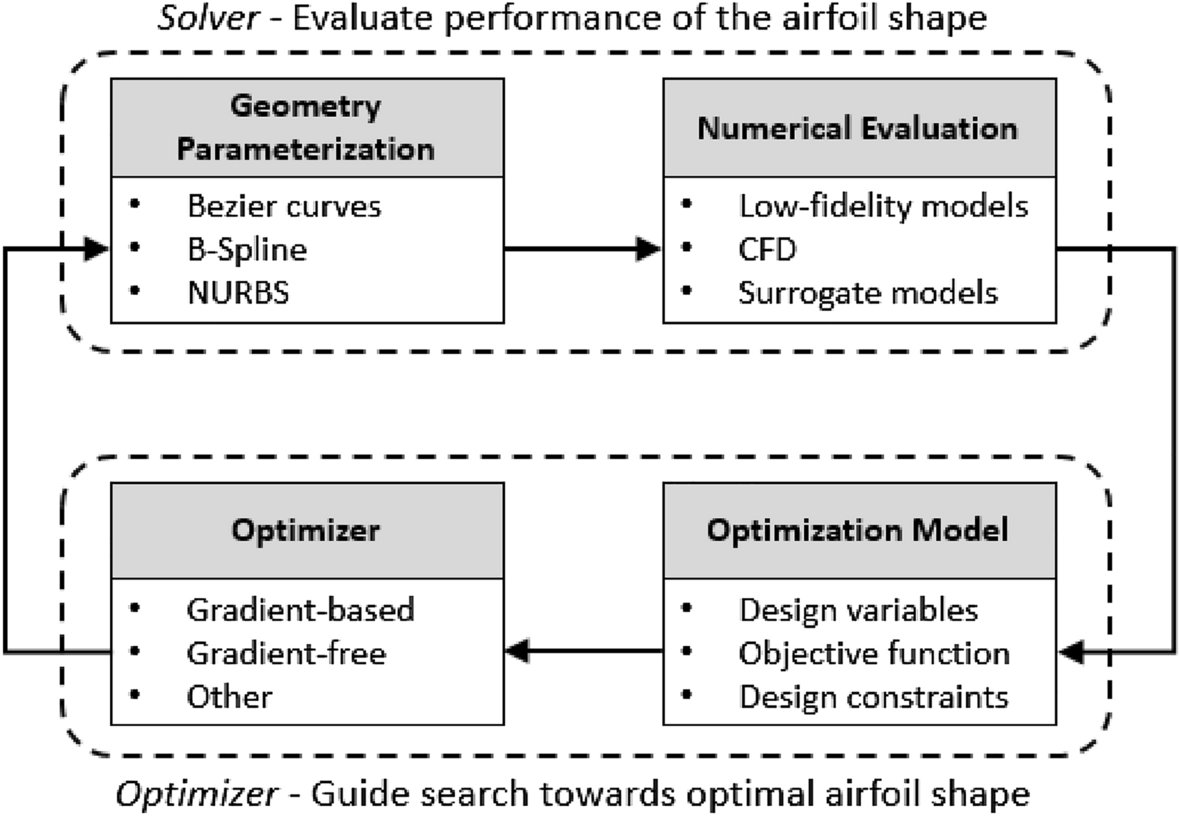
A reinforcement learning approach to airfoil shape optimization
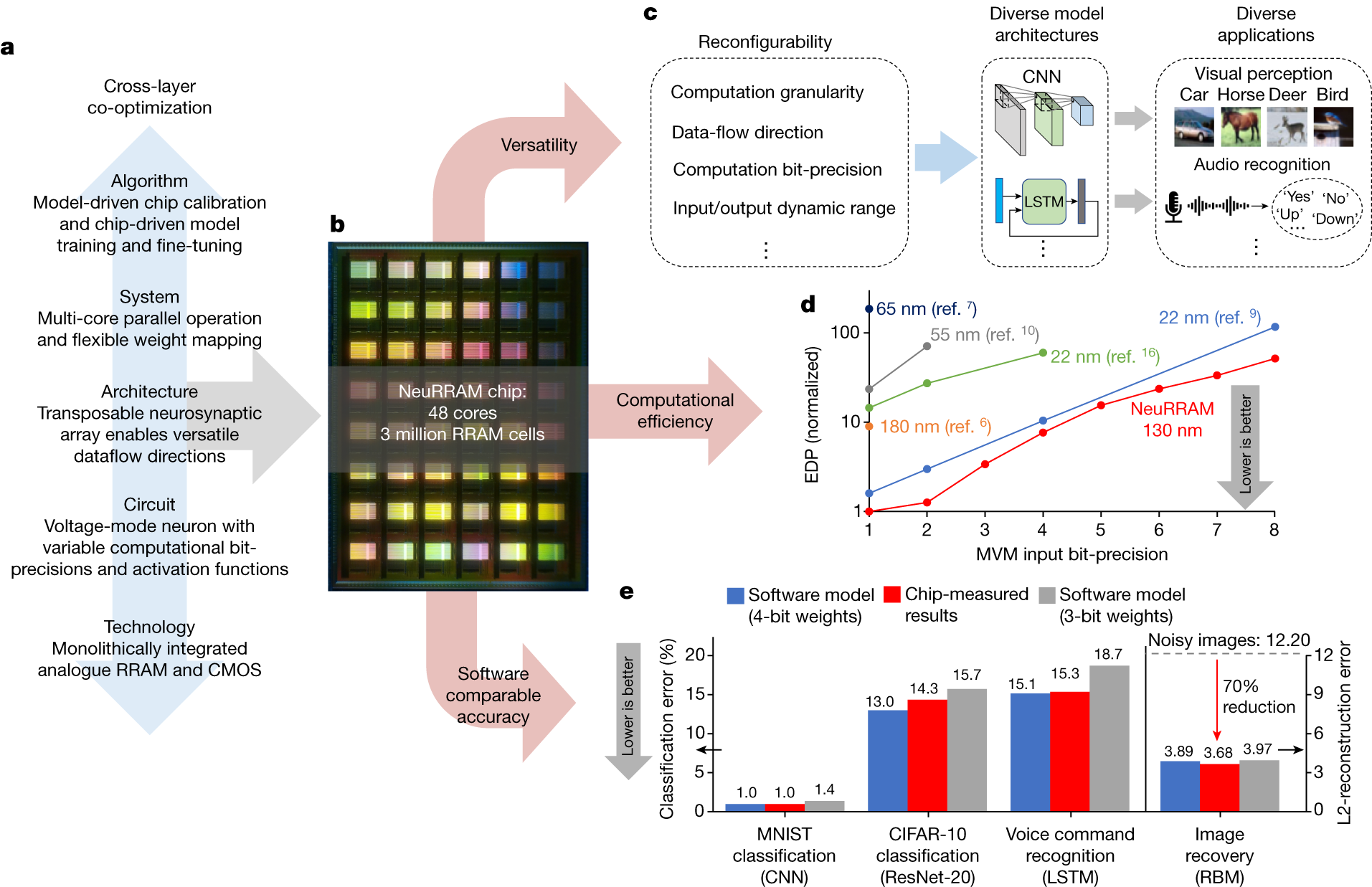
A compute-in-memory chip based on resistive random-access memory

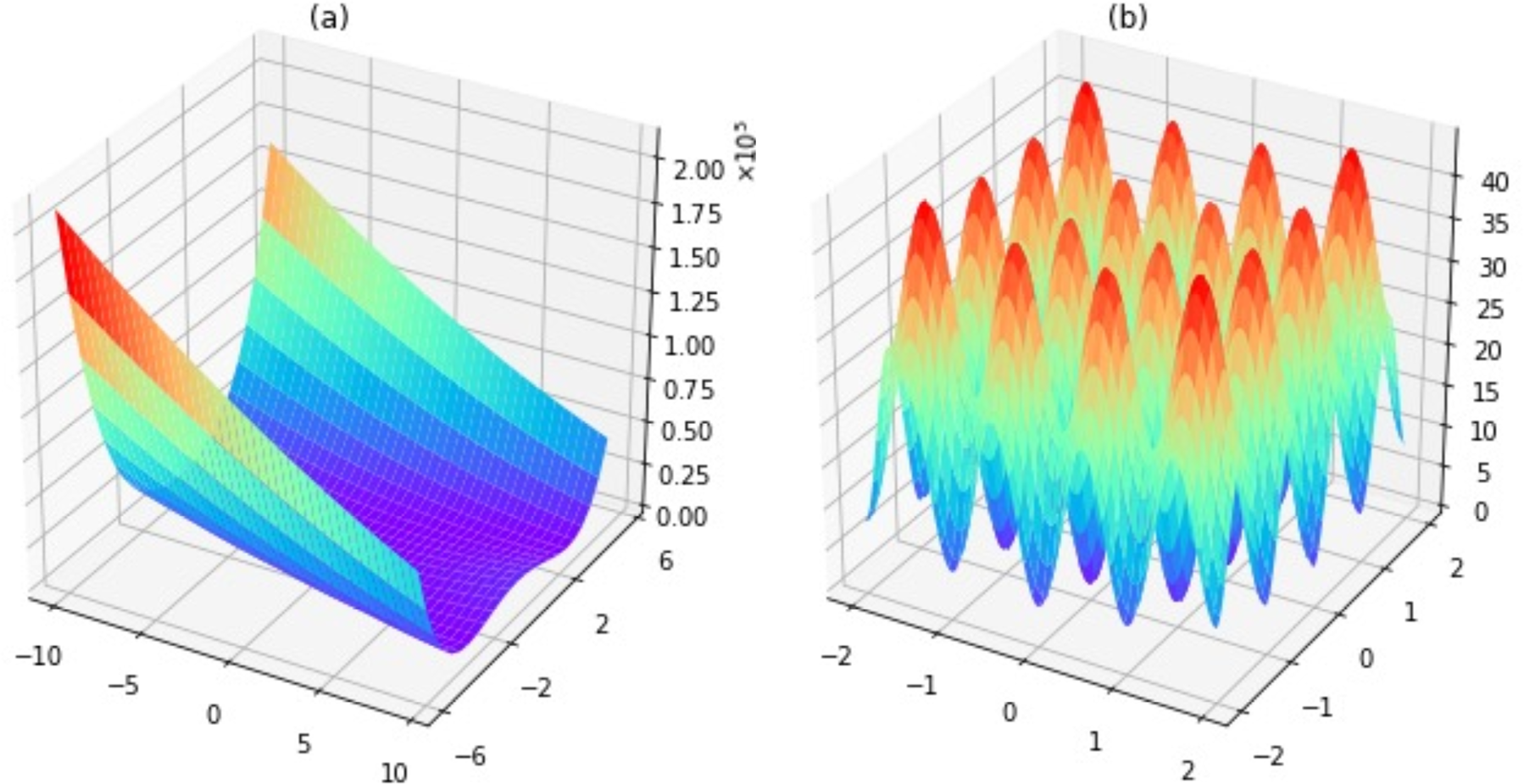
On q-steepest descent method for unconstrained multiobjective optimization problems

A Steepest Descent Method for Set Optimization Problems with Set-Valued Mappings of Finite Cardinality

Quasi-Newton methods for topology optimization using a level-set method
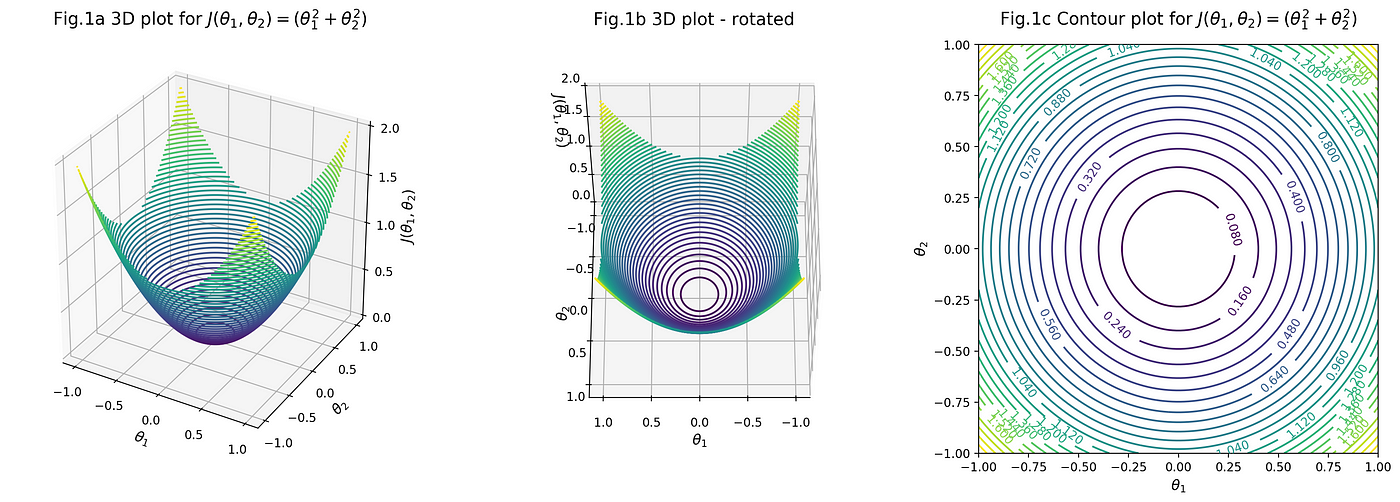
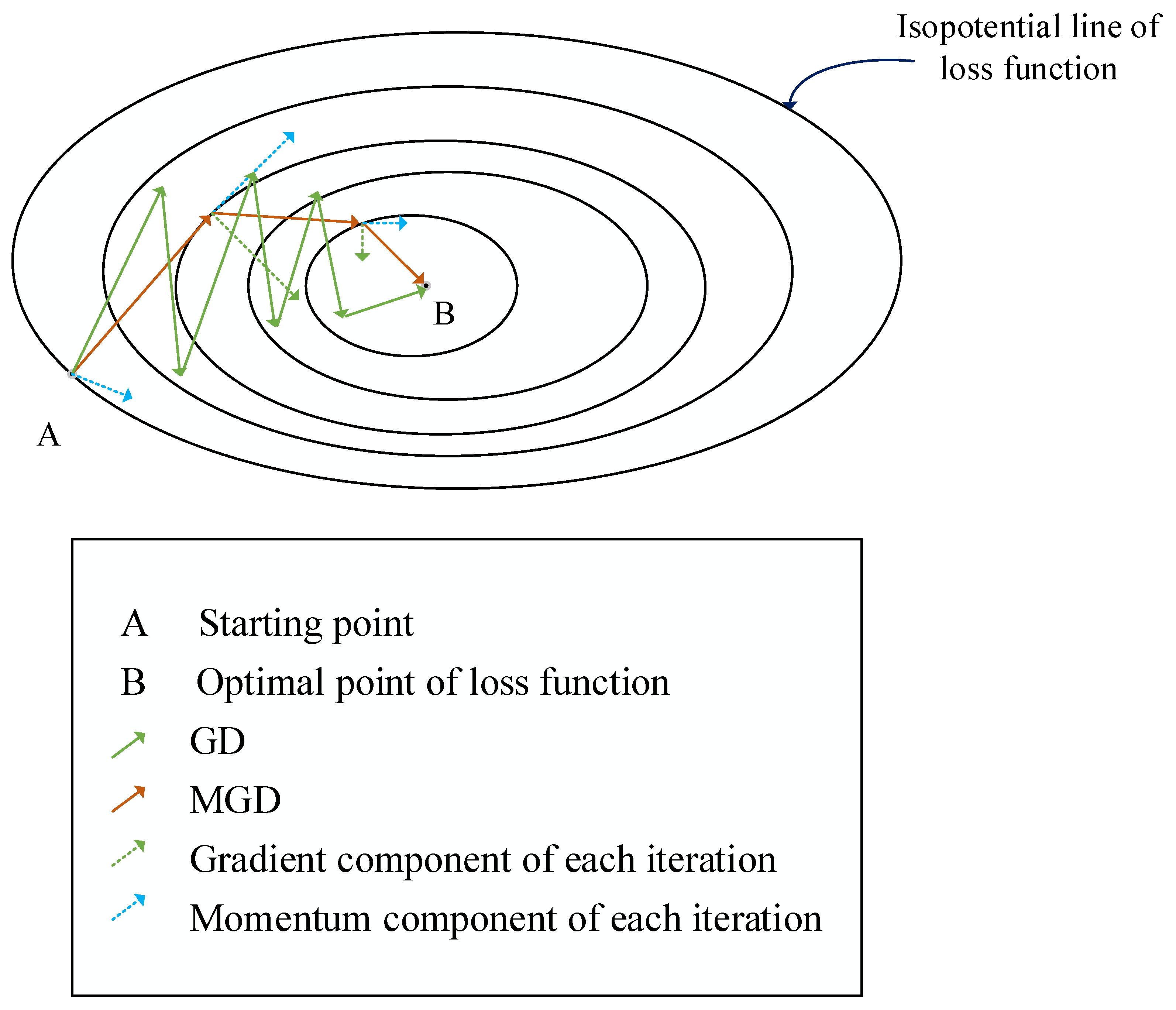
Intuition (and maths!) behind multivariate gradient descent, by Misa Ogura
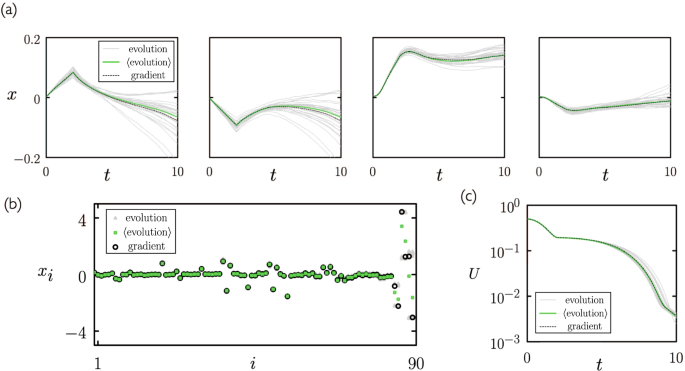
Correspondence between neuroevolution and gradient descent

Steepest Descent Method - an overview